Biography
Krissina (Krissi) Alari is a graduate student in the Statistics MA program at University of California, Berkeley. Her interests include applications of Bayesian statistics, generalized linear modeling, machine learning, and data visualization.
Previously, she attended California State University, Monterey Bay where she majored in mathematics and minored in statistics. Her undergraduate research focused on applying Bayesian inference to frequentist methods for measurement comparison studies. She also has work experience in statistical consulting. Her projects utilized statistical methods to address concerns and answer research questions in agricultural and environmental studies.
Outside of statistics and data science, Krissi also enjoys baking, yoga, and taking care of her succulent garden.
Download her resume.
- Bayesian Inference
- Generalized Linear Models
- Machine Learning
- Data Visualization
MA in Statistics, 2022
University of California, Berkeley
BS in Mathematics, Statistics Minor, 2021
California State University, Monterey Bay
AS in Mathematics, 2019
Chabot College
Skills
Experience
- Provides data science and statistics consulting to graduate students, visiting scholars, and UC Berkeley staff
- Specializes in providing guidance in the areas of model selection, implementing cross validation, and statistical programming techniques
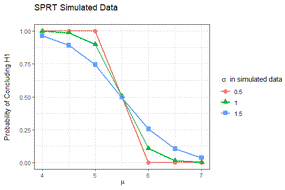
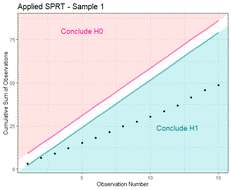
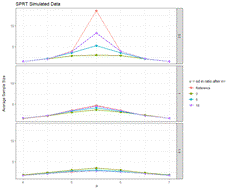
- Implemented sequential testing for bacteria testing procedures at local farms, which reduced sample sizes and improved efficiency up to 87%
- Developed an interactive R Shiny applet that guides users through their statistical analysis
- Produced a technical report that outlined statistical methodology, simulation results, and applied examples
- Presented research at the 2021 CSUMB Math/Stat Capstone Festival
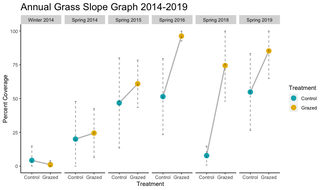
- Collaborated with biologists to study experimental plant groups using nonparametric statistics
- Compiled and cleaned six years’ worth of research data using R and Excel
- Created data visualizations for reports and presentations using ggplot2
- Provided instructional support for courses in introductory statistics and generalized linear models
- Collaborated with professors and co-workers to evaluate the efficiency and accuracy of student work
- Graded and provided feedback for 40-80 R programming assignments weekly
- Constructed data simulations in R to study the behavior of statistical methods
- Published a manuscript on the application of Bayesian statistics to measurement comparison studies
- Developed an interactive R Shiny web applet that produces analysis results, interpretations, and visualizations
- Presented research at the CSU Monterey Bay Spring Research, Scholarship, & Creative Activity Showcase
Data Visualization Gallery
